What are Sets?

A set of well-described objects in mathematics is a set that is called a proper unit. There was a misunderstanding. The most basic features are that a set of “has” elements and that two sets are identical (the same) if each of the elements is one element.

Set A contains the even numbers from 1 to 10 inclusive. Write this as a set. The elements of this set will be 2, 4, 6, 8, 10, so we write: A = {2, 4, 6, 8, 10}

The Number of Elements in a Set:

A collection of mathematically well-defined objects is a group called the right array. There’s been an incomprehension. The key characteristics are that one set of elements is “has” and two sets are the same (the same) if each element is one.

Sets of Numbers and Cardinality You should be familiar with the following special sets.

Natural (counting) numbers: ℕ = {1, 2, 3, 4, …}

Whole numbers: W = {0, 1, 2, 3, 4, …}

Integers: ℤ = {…, –3, –2, –1, 0, 1, 2, 3, …}

Rational numbers: ℚ = Irrational numbers: {x | x cannot write as a quotient of integers}.

Real numbers: ℝ = {x | x can be expressed as a decimal} and are integers, with 0 p p q q q ì ü í ý ¹ î þ

To show that a particular item is an element of a set, we use the symbol ∈. The symbol ∉ shows that a particular item is not an element of a set.

Definition: The number of elements in a set is called the cardinal number, or cardinality, of the set. This is denoted as n(A), read “n of A” or “the number of elements in set A.”

Example. Find the cardinal number of each set.

(a) The set A of counting numbers between ten and twenty.

(b) Set B of letters in the word “bumblebee.”

(c) C = {x|x is an even multiple of 5 that is less than 10}

Check out also: CONGRUENCE AND SIMILARITY

Universal Set and Subsets:

The universal set, ξ, for any problem is the set which contains all the available elements for that problem. The complement of a set A, A′, is the set of elements of ξ which do not belong to A.

The universal set is all of the odd numbers up to and including 11. ξ = {1, 3, 5, 7, 9, 11}

If A = {3, 5} and the universal set is the same as the previous example, write down the complement of A.

A′ = {1, 7, 9, 11}

The Universal Set denoted by U is the set of all possible elements used in a problem.

When every element of one set is also an element of another set, we say the first set is a subset.

C is a subset of When two sets have the same objects or elements in the first set, then the second set always includes elements.

is not a subset of at least one element is not a member of the second set of the first set?

Example A= {1, 2, 3, 4, 5} and B= {2, 3}

We say that B is a subset of A. The notation we use is BC A.

Let S= {1,2,3}, list all the subsets of S.

The subsets of S are 0, {1}, {2}, {3}, {1,2}, {1,3},

{2,3}, {1,2,3}.

Check out also: Properties Of Circle

Equal Sets:

It is said that two sets A and B are identical if they have precisely the same elements.

The sub-sets (denoted by C) are also two equal sets.

A= {2,4,6,8}           B= {8,6,2,4}

Then

A=B      B=A      A C B      B C A

Proper Sets:

If each part of a set A also appears to be part of a set B, but set B has more parts than set A, then set A is a proper subset B, which is referred to as “A c B.” So set B is not a correct subset of A (B A) in this case

C is a Proper subset of one each of the elements is also a second set in the first, but there are more elements in the second set than the first.

C is not a proper subset: if at least one element in the first set is not in the second set.

E.g. A = {1, 5, 9}     B = {1, 3, 5, 9}

Therefore:    A C B,      B  A

Intersection Sets:

A set containing all elements of A that also belong to B (or similar, all elements of B belonging to A) is the intersection of two sets A and B, denoted by A bis B).

A= {1,2,3,4,5,6}

B= {2,4,8,10}

AB = {2,4}

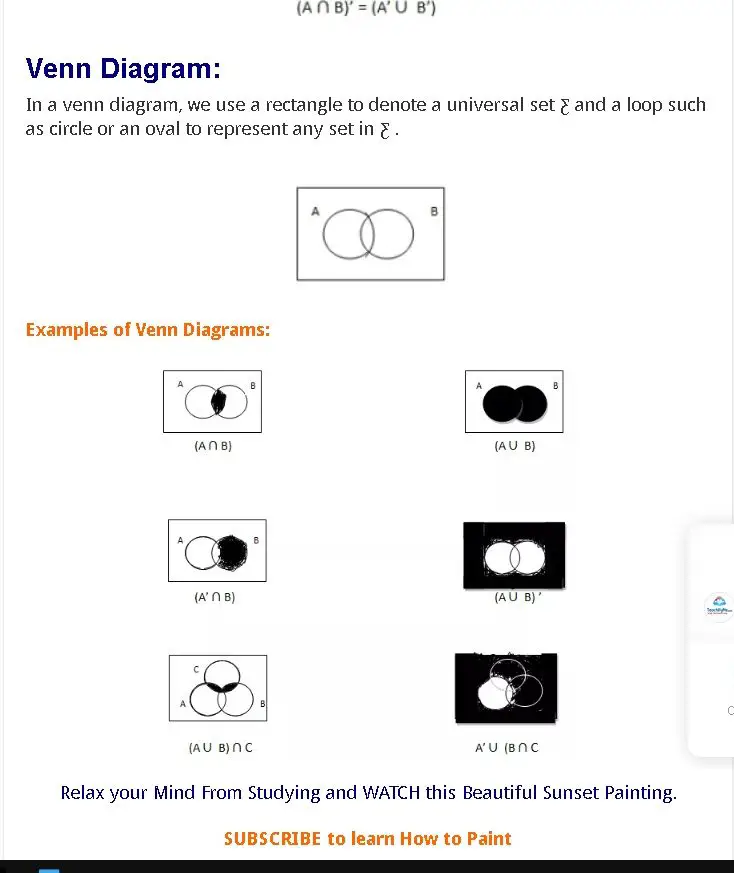
Venn Diagrams: