The essential fundamental figures in geometry are the lines and circles. We know a line is a locus of a point moving in a constant direction while the circle is a locus of a point traveling from a fixed point at a constant radius.
The circle ‘s abstract value is expressed in the amount of impressive applications
What is a Circle?
A circle is a shape composed of all points in the plane, which are a certain distance from the center of the point; in other words, a curve is drawn by a point traveling in a field to a fixed distance from a certain point.
| Terms | Description |
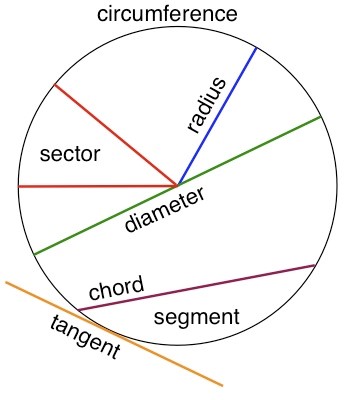
| Circumference
Radius
Diameter
Arc
Sector
Chord
Tangent
Secant
|
The circle boundary is considered the circumference
The radius is the line from the center “O” of the circle to the circle and is denoted with “r”
The line through the middle of the circle which reaches the two points is called the diameter and is marked with the sign “D”
Arc’s part is called the main arc, and the little arc is called the small arc the largest arc;
Sector is a segment of a sphere with two radii and an arc of a sphere
A chord is the straight line between two points in a circle The tangent is a line touching the circumference of a circle at a point.
A line in two distinct points that cuts the circle is called secant |
Check out also: Mensuration
Circle Properties
The following are some of the main features of the circle:
- The rings are said to have the same radius.
- A circle’s diameter is the longest round chord.
- The equal circumference of equal chords and equal circles.
- The circle drawn by the chord splits the chord.
- There are identical circles of different radius.
- Within a line, triangle and dance can be engraved a circle.
- The chords are equal to the duration of the middle.
- The difference between the middle of the circle and the longest chord is zero.
- When the chord length increases, the perpendicular distance from the circle center decreases.
- The tangents are drawn parallel to each other at the end of the diameter.
- The radii that link a chord to the middle of a circle form an isosceles triangle.
Check out also: Numbers
Circle Formula

Area of a circle: A = πr2 square units
The circumference of a circle = 2πr units
The circumference of a circle formula is also written as πd
Where,
Diameter = 2 x Radius
D = 2r
Here “r” represents the radius of a circle.

