A vector has magnitude (size) as well as direction. In a graph, they are labeled with an arrow, in which the longitude of the arrow informs us of the size and the direction of the arrow.

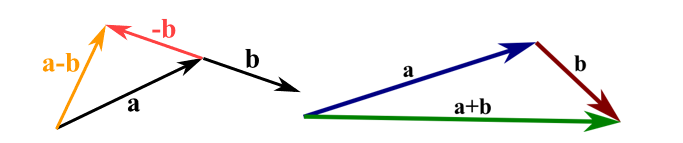
We add end-to-end vectors when we add them. For instance, when you add two a and b vectors, then you get the result of a+b which takes you from a to b at the end.

The vector’s negative is equal to the original vector, and it only goes exactly the other direction. As subtracts vectors, such as a−b, add to the negative of the subtracted vector, i.e. adding the vector -−b to a vector as seen in the image.

One vector can be multiplied by one. It is the same as adding several multiples to itself as with usual multiplication, and the consequence of multiplying by 3 is therefore

3a = a + a

Then, the end-to-end is inserted, just as we saw before. Note: here are all the vectors in bold. You should emphasize each letter which represents a vector when you write this by hand.

Often vectors are divided into two parts – an xx part which tells us how far the vector goes to the right or to the left and a yy part which tells us how far a vector goes to and from.

It is important to note that the vectors you see are just different ways in which the diagrams and vectors are written in columns. Suppose you have two vectors on your board, which you add to get a different vector.

The resulting vector would be exactly what you got if you had added both the column vectors to a graph and added them end-to-end (as we saw above).

For example, the vector goes up three spaces to the right and 2 to the right (3/2). If the function goes to the left, the xx value is negative, and the yy value is negative if it goes down.

We add/subtract xx and yy values separately in order to add/subtract column vectors. For instance,

(−10) + (2 / 6))

To multiply a vector column by a number, we multiply all values by this number in the row, for example.

Check out also: Vectors

5 * (2 /−3) = (10/-15)

PARALLELOGRAM LAW:

If the opposite sides of a point-drawn parallelogram represent two vectors acting concurrently at a point, the resulting vector is seen in magnitude and direction both by the diagonality of the parallelogram that passes by that position.

DERIVATION OF LAW:

Let P and Q be two vectors that act at one point simultaneously, both in magnitude and direction represented in the figure, by two adjacent sides OA and OD of an OABD parallelogram.

The resulting vector should be the angle between P and Q and R. Diagonal OB then represents the resulting P and Q, according to vector addition’s parallelogram law

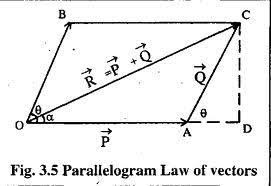
So, we have

R= P+Q

Now, expand A to D and Draw CD Perpendicular to OD

From triangle ODC,

OC² = OD² + CD²

Or         OC² = (OA+AD) ² +CD² ………   (i)

In triangle ACD

Cos = AD/ AC

Or        AD = AC cos

Or        AD = OB cos   = Q cos

Also,

Sin = BD/ AC

Or        AD = AC Sin

Or        AD = OB Sin = Q Sin

Check out also: Trigonometry

MAGNITUDE OF RESULTENT

Substituting the value of AD and AC  in  (i), we get

Numeric Problem