Congruence
It is believed that two forms are congruent in type and dimensions: the respective sides of the two shapes are equal in weight, and the correct angles are similar.
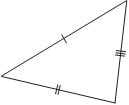
There are two congruent triangles.
Shapes in different sizes, but the same form, are claimed to be identical.
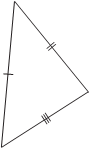
The triangle below is close to the above triangles, but it does not equate to the above triangles since it is a different dimension.
Four measurements are described below for congruence.
Check out also: BEARINGS
Test 1 (Side, Side, Side)
If the three faces of one triangle are the same as the faces of the 2nd triangle, the two triangles are identical. The test is referred to as SSS.
Test 2 (Side, Angle, Side)

If the two sides of a triangle are the same length as the two sides of the other triangle and in the two triangles the angle between them is the same, the triangles are congruent.
Check out also: MATRIX
Test 3 (Angle, Angle, Side)
If in both triangles the two angles and length on one side are the same, the two angles are congruent.
This test is referred to as AAS.
Test 4 (Right Angle, Hypotenuse, Side)
When all triangles have a right angle, hypotenuses are equal in length and the other hand is similar in length they are congruent.
This test is referred to as RHS
SIMILARITY
Like congruence, similarity includes the identification of two objects. However, the proportions do not have to be close to a resemblance.
There are a few implications here. First, while two congruent objects must also be similar, two similar objects do not need to be congruent, by definition.
The other is that if two objects are identical, the second is either an improved version (or also the same dimension, in which case the objects are both congruent) or a scaled-down variant of the first one.
All objects also vary in orientation and position, although this does not depend on whether or not they are identical. All circles have been close, we said earlier.
Furthermore, it should be very clear to see that all regular polygons of the same form are also identical.
The above triangles are also scalene triangles (i.e. triangles where no two edges are identical, and no two sides are identical).
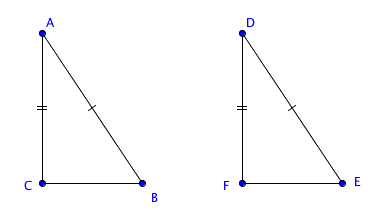
The two triangles (in fact, any two triangles) can be called similar if the respective sides differ in length by an equal proportion. This can be represented as: Concerning the ABC and DEF triangles
| AB | = | BC | = | CA |
| DE | EF | FD |
The two triangles are also similar if two angles of each magnitude are the same (when the third pair of the corresponding angles is automatically equal because the inner angles of a triangle always amount to one hundred and eighty degrees): The two triangles are also similar:
∠ABC = ∠DEF and ∠BCA = ∠EFD
or:
∠ABC = ∠DEF and ∠CAB = ∠FDE
or:
∠BCA = ∠EFD and ∠CAB = ∠FDE
It can also be seen that two triangles are identical because two pairs of sides are equal in length and the angles are the same. Examples include:
| AB | = | BC | and ∠ABC = ∠DEF |
| DE | EF |
or:
| BC | = | CA | and ∠BCA = ∠EFD |
| EF | FD |
or:
| CA | = | AB | and ∠CAB = ∠FDE |
| FD | DE |
If the ABC and DEF triangles were identical, the resemblance symbol (~) may be used to show this:
ΔABC ~ ΔDEF

