The turning effect of a force is known as the moment. It is the product of the force multiplied by the perpendicular distance from the line of action of the force to the pivot or point where the object will turn.
When undoing a nut fastened to a screw by hand one realizes that the amount of force required is a lot greater than when undoing the same nut using a spanner. The spanner increases the distance between the fulcrum and the line of action of the force, thus for the same force a greater moment is obtained.
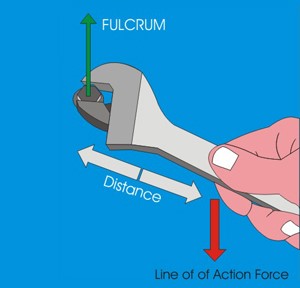
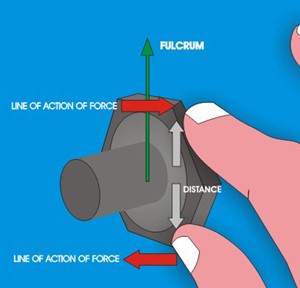
| SMALL MOMENT The distance from the fulcrum to the line of action of force is very small |
LARGE MOMENT The distance from the fulcrum to the line of action of force is large |
Read also: Transfer of Thermal Energy
Principle of Moments
The principle of moments states that when in equilibrium the total sum of the anti-clockwise moment is equal to the total sum of the clockwise moment.
When a system is stable or balance it is said to be in equilibrium as all the forces acting on the system cancel each other out.
In equilibrium
Total Anticlockwise Moment = Total Clockwise Moment
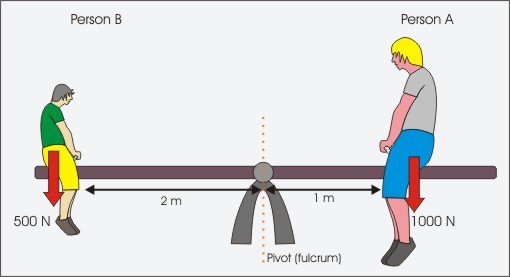
This principle can be explained by considering two people on a seesaw.
Moments Acting on A Seesaw
Both people exert a downward force on the seesaw due to their weights.
Person A’s weight is trying to turn the seesaw anticlockwise whilst person B’s weight is trying to turn the seesaw clockwise.
Person A’s Moment = Force x perpendicular distance from fulcrum
1000 x 1 = 1000 Nm
Person B’s Moment = Force x perpendicular distance from fulcrum
500 x 2 = 1000 Nm
Persons A’s moment = Persons B’s Moment
Anticlockwise moment = Clockwise moment
Need Help? Ask Our Chat Assistant!
-
Hi, I am your Assistant & here to help you out with your preparation, Ask me anything!
Therefore, seesaw is in equilibrium.
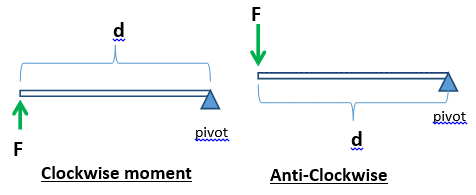
Moment = F x d
F: Force applied
d: Perpendicular distance from the force to the pivot
- In equilibrium, total clockwise moments = total anti-clockwise moments about the same pivot.
- Clockwise = Anti-Clockwise
Centre of Gravity
- Defined as the point whereby the entire weight of the object works and is equivalent for all directions.
- Note: the CG doesn’t have to be inside the object (e.g. Donut)
- A lower CG increases model stability
- The targets are more robust with a greater base region
- How can the CG be located and where can it be found?
Read also: Practical Electricity
Stability:
- secure equilibrium: after a little displacement, the object returns to its original location
- The Neutral Balance: The subject is in the same position though it has been marginally displaced
- Towards precarious balance: the object overturns after it has shifted very
