Energy, Work, Power

Work and Energy:

Energy is required to move, form, and warm up stationary objects. The energy is moved from the muscle to the object as one takes up an object.

Objects can possess energy in terms of the following:

• Gravitational potential stores
• Kinetic waves
• Thermal stores
• Elastic stores

Energy can be transferred between different objects in different ways:

• Radiation
• Electrical
• Mechanical

The energy in Joules (J) is calculated. 1 Joule= energy required to increase weight 1N by 1-meter vertical height.

Whenever energy is transmitted, energy is transferred to total after = energy total before transmission. Complete energy is equal.

Principle of conservation of energy.

Forces:

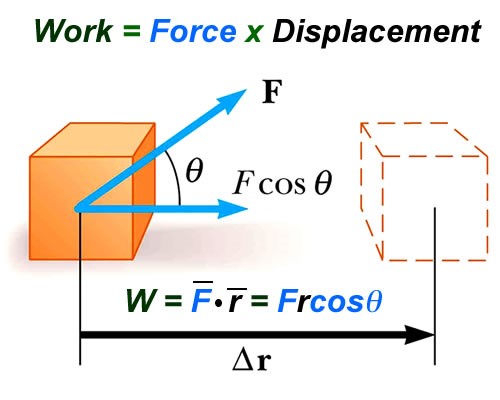
• Work is done on an object when a force acting on it makes it move.
• Energy is transferred to the object.
• The amount of work done depends on the force and distance.
• The greater the distance, or force, the greater the Work Done.
• Work Done = Force × Perpendicular distance

Examples:

A force of 1 N is required to raise an object of weight 1 N steadily. If it is raised by 1 m, the work done by the force is 1 J (=1 N × 1 m)

For a 2 N object raised to a height of 1m, the work done and potential energy of the raised object is 2 J (=2 N × 1 m)

Work Done = (Force distance) ×Cosθ

If θ = 90°, then Work done = 0 

Force-Distance Graphs:

Read also: Electromagnetic Induction

Constant force:

Constant force F acts on an object and makes it move a distance s in the direction of the force, the work is done on the object: Work done=Force × Distance of force

A graph of this constant force will produce a rectangle, the height will represent the force and the width will represent the distance, and hence the area = Work Done

Therefore,

the area under the line = Work Done

Variable force:

If a variable force acts on an object and causes it to move in the direction of the force, the Work Done for a small amount of distance (Δs), ΔWork Done = Force × Distance

Represented on a graph of Force (F) against distance (s) by the area of a strip under the line of width Δs and height F

Total work is done = ∑area of all strips.

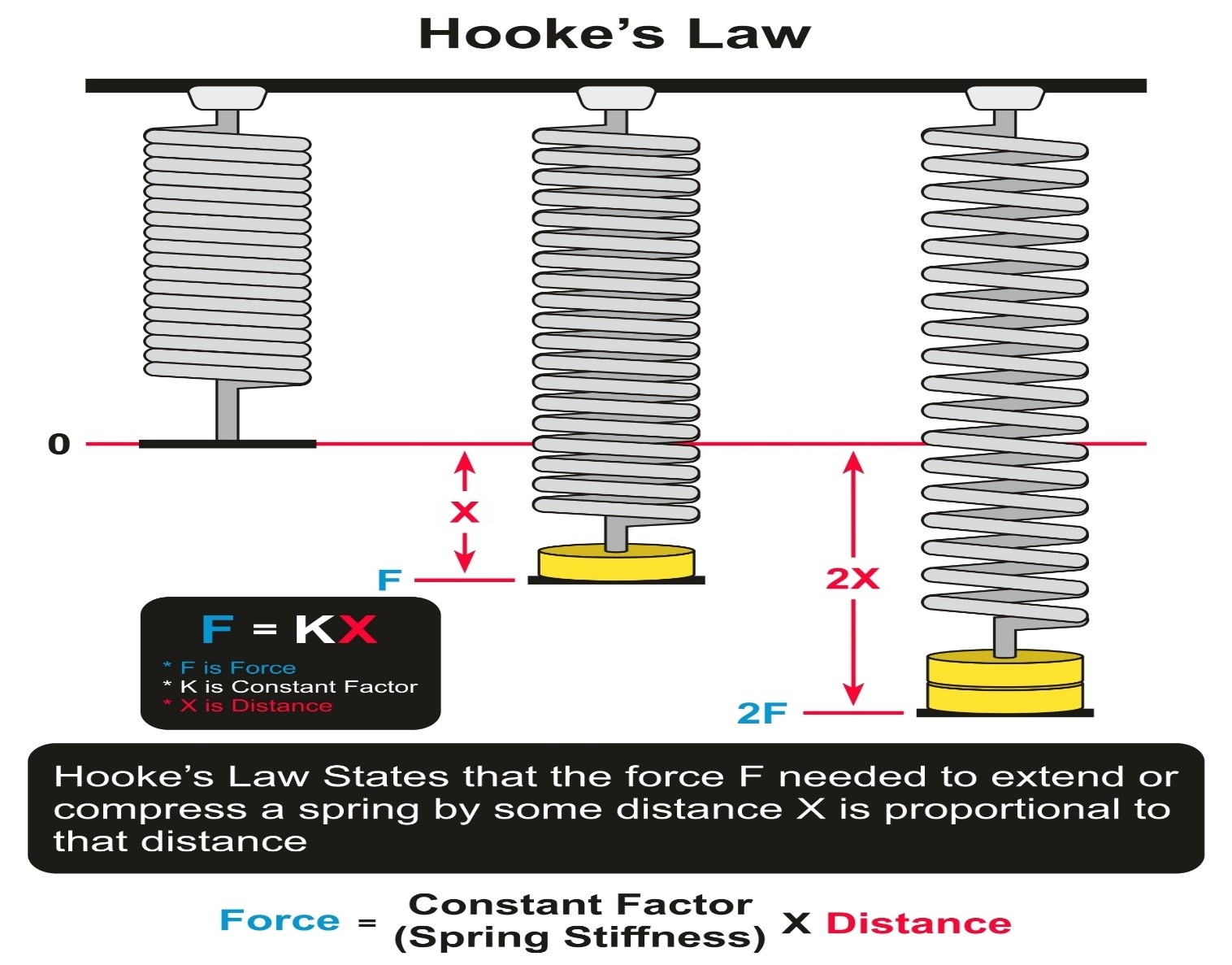
Consider the force needed to stretch a spring.

The greater the force, the more the string is extended from its unstretched length.

The diagram below will show you how the force needed to stretch a spring changes with the extension of the string.

The graph is a straight line through the origin.

Therefore, the force needed is proportional to the extension of the spring:

Hooke’s Law

The diagram below is a Force against distance or the distance the spring is stretched.

Therefore, the area under the line represents the work done to stretch the spring.

As the graph is a triangle, the work done is = ½FΔL

Power:

Energy from one entity to another may be transferred:

• Function by force when one object pushes the other.
• The diffusion of heat from a hot subject to a cold object. Driving, convective, or radiation can contribute to heat transfer.
• In comparison, energy can be transmitted by electricity, sound, and EM waves like a light.
• In any transmission process, the higher the power of the transfer process, the more energy is transmitted per unit of time.
• The most efficient elevator in a tall building is the one that hits the roof the shortest, with two equal-size elevators.
• Simpler, the engine transfers power more easily than the engine on the other lift.

Power is defined as the rate of transfer of energy.

The unit of power is the watt (W), equal to an energy transfer rate of 1 Joule per second.

1 Kilowatt (kW) =1000W

1 megawatt (MW) 1,000,000 W

If energy ΔE is transferred steadily in time: Δt:

Then:

Power = ΔE/Δt

Where energy is transferred by a force doing work, the energy transferred =work done by the force.

Therefore, the rate of transfer of energy is =work done per second.

Power P =ΔW/Δ t

Deriving P=f v:

P=W/t

W=Fs

Therefore P=Fs/t

But V=s/t, or Vt=s

Therefore Power= Force × velocity × time/time

Therefore Power =F v

Muscle power:

The gain of potential energy= Weight × total height gain

Muscle power= energy transferred/time taken    =      weight ×height gain/time

Example:

A person of weight 480N who climbs a flight of stairs of height 10m in 12 seconds, has leg muscles of power 400W (= 480N × 10m / 12 seconds)

Therefore, each leg has the power of 200W

Electrical power:

The power of a 12V light bulb can be measured through a joulemeter.

Joulemeter read before and after the light bulb is switched on.

The difference between the readings is the energy supplied to the light bulb.

If the light bulb is switched on for a measured time, the power of the light bulb can be calculated from: Energy supplied / time is taken.

Engine power:

Vehicle engines are designed to make objects move.

The output power of an engine is called its motive power.

(When a powered objective moves at a constant velocity at a constant height, the resistive forces are equal and opposite to the motive force.)

Work done by the engine is transferred into the internal energy of the surroundings by the resistive forces.

For a powered vehicle driven by a constant force of F moving at the speed of V

The work done per second = force × distance moved per second.

When a powered object gains speed, the output force exceeds the resistive forces on it.

Consider a vehicle on a level road.

The output power of the engine is the work done by the engine per second

Work done by the engine increases the kinetic energy of the vehicle and consequently allows the vehicle to overcome the resistive forces acting upon it.

Therefore:

Motive power= energy per second wasted due to resistive forces + gain of kinetic energy per second.